Brackets, Orders, Division/Multiplication, Addition/Subtraction: The basic problem of mathematics

Every day, situations arise in which mathematics is critical. Unfortunately, it is not always as simple as addition and subtraction, especially when performing multiple mathematical operations on a single number in the sequence. For simple arithmetic, the order of operations is unimportant; however, for more difficult problems, errors are frequently made because the incorrect order of operations is followed. Fortunately, some rules govern which mathematical action should always be taken first in any given situation. These are known as brackets, orders, division/multiplication, and addition/subtraction (BODMAS) rules.

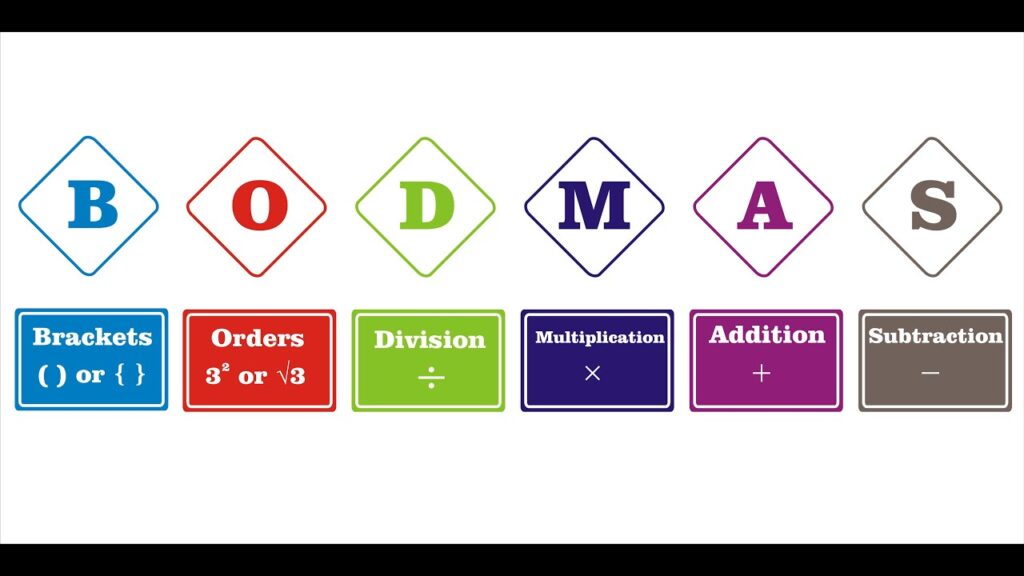
In mathematics, the operation’s order is the BODMAS rule (brackets, orders, division/multiplication, addition/subtraction). Bodmas is used to solve arithmetic problems.

According to the rule, multiplication and division come before addition and subtraction. This means that you can’t just add or subtract things unless they’ve already been multiplied or divided.

• Operators in the lower bracket take precedence over that outside of it. 5+3*2 is one example. Because 2*3=6, it should calculate to 11, which equals five plus three times two, so 3 takes precedence over * when doing the calculation inside the brackets.

• However, if there is a division in the brackets, it will be performed first because division takes precedence over multiplication. 5+3/2 should equal 4 because 5/2=2.5 and 3/2=1.5.

• When there is more than one set of brackets, the numbers inside them are calculated in turn, so the calculations can be done from left to right, making sure that everything is done correctly before moving on.

• In mathematics or algebra, no matter what comes after an equal sign (=), one does not need to follow BODMAS because = takes priority and equals are always calculated first.

• This is true even if the equal sign is followed by a division symbol (/). It simply means that whatever is on one side of the = must be equal to whatever is on the other, so 1/2=4 would be 1/(2*4)=1/8.

• The same is true for the (+ and -) addition and subtraction symbols. If a = has more than one side, it is calculated from left to right, just like brackets. 24 would become 5-(-1)=6 because the numbers on the right are calculated first, and whatever is left is moved to the equal sign after that.

• Brackets are another application of BODMAS in mathematics and algebra. Calculations inside brackets () can be performed in any order by following BODMAS to obtain the answer. For example, 3+2*3-1 becomes (3+2)*3-(1), which equals nine because * takes precedence over + and -, so the 2 is multiplied by 3 before being added to one.

• It can also be used for inequalities such as >, >=, and =. All you have to remember with them is that greater than > takes precedence over which takes precedence over >=because it’s the same symbol but written sideways.

• Less than takes precedence over =, which takes precedence because it is the same symbol written sideways. If there are more than one of either > or, they are worked out in the same order as everything else, from left to right.

• Another thing about inequalities is that they can be made negative by using a minus symbol (-). 5-2 would become (5(-2)+(-2) It is calculated as 5-4, which means that five cannot be less than four.

Bodmas teach students about zero pairs (negative numbers that add up to zero) and how to simplify fractions by dividing both top and bottom by a common factor without canceling anything. This is how the Order of Operation is carried out.

BODMAS rule, in essence, uses brackets to indicate the order of operations. Brackets are used to hide or override the standard precedence rules, but they do not affect the final result. When a learner uses the cuemath website to learn math, it becomes second nature to him. Cuemath is the ideal solution for any math problem.